Tabular Rsines from the properties of chords in Indian astronomy
Dr. Vanishri Bhat
Asst. Professor
Chanakya University, Bangalore-
Email: vanimanju2020@gmail.com
Abstract
Finding methods for obtaining accurate values of tabular Rsines called Jyānayana or Jyotpatti has been an important topic in Indian astronomy that made astronomers to compose short texts exclusively on this topic. Bhāskarācārya-II dedicated a whole chapter for finding tabular Rsines. Reckoning time from the true position of planets with the background stars was based on the determining accurate sine values. Hence, in order to improve the accuracy of the values of sine function, there has been continuous effort starting from the Siddāntic period, till the end of the medieval period. The earliest text that presents a recursive relation for constructing sine table is Āryabhaṭa’s Āryabhaṭīya, which prescribes a formula for obtaining the first order sine differences.
In my paper I will discuss another interesting approach of constructing a recursive relation form the properties of chords presented by Śaṅkara Vāriyar (c. 16th century) in his detailed commentary Kriyākarmakarī on Līlāvatī of Bhāskarācārya. Śaṅkara’s approach for constructing sine table is based upon the interesting properties obeyed by the chords of a circle, that may be called jyā-saṃvarga-nyāya and jyā-vargāntara-nyāya which is quite different from the approach suggested by Āryabhaṭa. Keywords: Jyotpatti; Rsines; Śaṅkara Vāriyar; Kriyākramakarī, jyā-saṃvarga-nyāya
Introduction
The need for finding precise values of sine function, generally referred to as jyās arose in ancient India in connection with the astronomical calculations. In order to capture the irregular motion of the Sun, the Moon and the celestial bodies, the Indian astronomers had constructed geometric models. The accuracy of predicting longitudes and latitudes using such models was heavily dependent on the accuracy with which they could compute the jyās. This explains as to why these concepts got developed in ancient India. Though it can not be exactly dated as to when did the search began, one can certainly say that during the Siddhāntic period (early part of previous millennia), the concepts of sines and cosines had got well developed.
1.1 The concept of jyā, koṭi and śara
In this section, I would like to introduce some technical terms that would be frequently used in the paper. In Figure 1, the arc ADC is called cāpa as it looks like a bow and the chord ABC is called the jyā. Literally the word jyā refers to a rope or a string and it is quite meaningful to use this term to refer to the chord ABC as it connects the two ends of the bow (dhanus) ADC. Some of the synonyms for jyā are guṇa, śiñjnī, mayyurī, jīva. OB is called as koṭi. Since BD looks like an arrow attached to the string ABC, it is called as ´sara. Śara also called as utkramajyā. The list of these technical terms along with their modern mathematical notion are given in the Table.1.

Figure 1: Diagram explaining the terms jyā, koṭi and śara
Indian names for trigonometric functions Equivalent modern expressions
1. ज्या/भुजाज्या R sin θ
2. कोटिज्या R cos θ
3. शरः/उत्क्रमज्या R − R cos θ
1.2 Jyotpatti or Jyānayana
The method for obtaining the tabular Rsines is technically referred to as Jyotpatti or Jyānayana. This is one of the most important topics on which one will find discussion in every text of Indian astronomy. There had been continuous efforts on the part of astronomers to improve the accuracy of the Rsine values. Though one of the earliest systematic treatment on Jyānayana is to be found in Āryabhaṭīya of Āryabhaṭa (476 AD), according to the renowned indologist Prof. R. C. Gupta, the invention of the sine function would have been much more earlier than Āryabhaṭa [5,1].
In his Āryabhaṭīya of Āryabhaṭa describes different approaches (geometric and analytic) to obtain tabular Rsines. Bhaskarācārya II (1114 AD) in his famous work Jyotpatti gives around five different methods to generate the sine table including methods prescribed by Brhamgupta [6, 27-29]. This paper discuss a novel approach to the construction of sine table using some properties of chords as given by Śaṅkara’s (c. 16 century) in his Kriyākramakarī, an elaborate commentary on Līlāvatī of Bhāskarācārya.
1.2.1 The motivation for accuracy of sine values
Indian astronomers put efforts obtaining accurate values of sines. As indicated earlier, this was because, the accuracy in the computation of sines → accuracy in the compilation of planetary positions → accuracy in the determination of solar months, lunar months, tithis etc., which in turn facilitated them to perform various religious and social observances at ‘appropriate’ times. In fact, as time was considered to be an integral part of their observances, performing something at an inappropriate moment would amount to not fulfilling the requirement of the observance, that was tantamount to incomplete performance. Incomplete performance would rather lead to adverse effects. This explains the motivation for evolving several methods of obtaining accurate sine values, one of which has been discussed in the current paper.
- Theorems on the chords of a circle
The present section deals with two theorems on the chords of a circle. These theorems are discussed by Śaṅkara’s Vāriyar in his Kriyākramakarī, in the context of investigating the area of a cyclic quadrilateral in detail in a chapter called Kṣetravyavahāra. It presents an interesting approach to the construction of sine table by means of a recursive relation. This recursive relation is quite different from the one presented by Āryabhaṭa, or the improvised versions of it presented by later astronomers like Nīlakaṇṭa (c. 1500). While the approach of Āryabhaṭa to jyānayana is based upon finding the first order sine-differences (called khaṇḍajyās), the method suggested by Śaṅkara Vāriyar is based upon a theorem satisfied by the chords in a circle. In the following sections we will explain how the tabular Rsines can be constructed based on this theorem called jyāsaṃvarga-nyāaya.
2.1 The jyavagāntara-nyāya: Theorem on the difference of the squares of chords
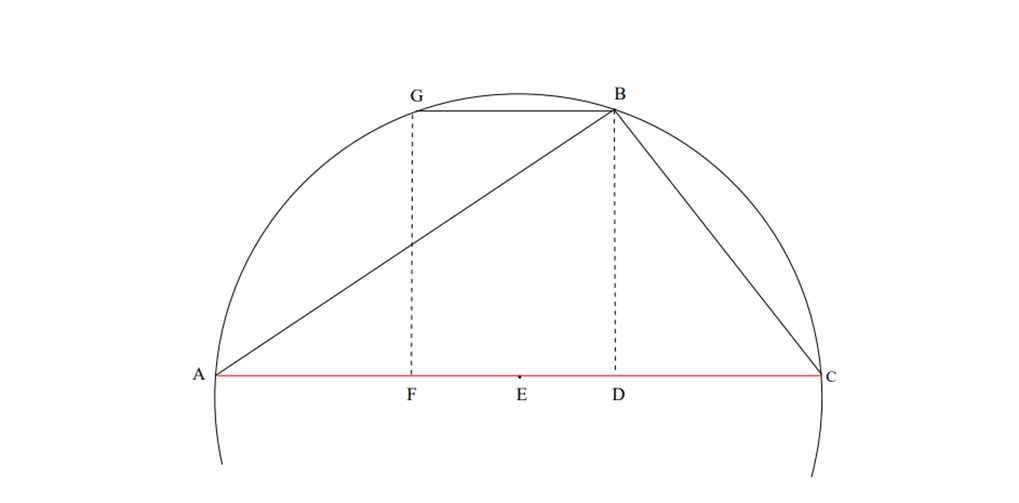
Figure 2: A triangle formed by three jyās to explain jyāvargantara-nāya
Śaṅkara Vāriyar’s explanation on the theorem on the difference of the squares of chords can be demonstrated with the help of Figure 2. Here AB and BC are two chords in a circle such that one of their end-points is common and coincides with B as shown in the figure. By joining the other two open ends A and C of the two chords the triangle ABC gets formed with the three segment AB, BC and CA, with CA as the base (bhūmi).
We now drop a perpendicular from the vertex B to meet the base CA at D, so that two right angled triangles ABD and CBD get formed. Using the bhujā-koṭi-karṇa-nyāya (the so-called Pythagorean theorem), the side BD, being common to both the triangles, can be expressed as
BD^2 =AB^2-AD^2
also
=BC^2-DC^2 (1)Hence we have,
AB^2-BC^(2 )= AD^2-DC^2
=(AD+DC) (AD-DC) (2)
Let F be a point chosen such that AF = DC. Hence,
AD-DC=AD-AF
=FD.
Having obtained FD, which in fact is referred to as ābādhantara , Śaṅkara Vāriyar says that this segment be slided above, parallel to AC, such that FD coincides with GB [1, 349]. It can be easily shown that GB is the chord corresponding to the difference of the two arcs ⏜AB and ⏜BC. For this, consider AB which may be expressed as:
⏜AB = ⏜AG+ ⏜GB
Or ⏜GB = ⏜AB- ⏜AG
= ⏜AB- ⏜BC (∵ ⏜BC=⏜AG) (3) Thus from (2), it can be seen that the difference of the squares of the chords is equal to the product of the chord corresponding to the sum of the arcs (AD +DC) and the chord corresponding to the difference of the arcs (AD−DC).
Denoting the arcs—referred to as cāpas in Sanskrit—corresponding to AB and BC as
c_1 and c_2, and the chords (jyās) corresponding to these cāpas as J1 and J2 (2) may be expressed as:
J_1^2-J_2^2=J (c_1+c_2 )*J (c_1-c_2 ). (4)The above theorem on the difference of the squares of the chords may be referred to as the jyā-vargāntara-nyāya. A corollary to this is the jyā-saṃvarga-nyāya, whose derivation is shown in the next section.
- The jyāsaṃvarga-nyāya: Theorem on the product of chords
For convenience in arriving at the desired expression, we now conceive of a slightly different problem. In Figure 2, we now consider the chords corresponding to the sum and difference of the two arcs ⏜AB and ⏜BC themselves given by AC and GB. The product of these two chords is given by
AC*GB =(AD+DC)(AD-DC)
=AD^2-DC^2
=AB^2-BC^2. (5)
The sum of two arcs ⏜AC and ⏜GB may be expressed as:
⏜AC+⏜GB= ⏜AB+ ⏜BC+⏜GB
=2* ⏜AB (∵ ⏜BC= ⏜AG )
Therefore,
⏜AB = (⏜AC+⏜GB)/2 (6)
Similarly, the difference of the arcs may be written as
⏜AC-⏜GB = ⏜AG+ ⏜GB+ ⏜BC-⏜GB
=2* ⏜BC (∵ ⏜AG= ⏜BC)
Hence,
⏜BC=(⏜AC-⏜GB)/2 (7)By definition, AB=J (⏜AB). Therefore,
AB=j (( ⏜AC+⏜GB)/2)
and
BC=j (( ⏜AC+⏜GB)/2) (8)Using (8) in (5) we have,
AC*GB=[J ( (⏜AC+ ⏜GB)/2)]^2- [J ( (⏜AC- ⏜GB)/2)]^2 (9) We may express the above result in a general form. If J_m and J_n be any tow chords (jyās) in a circle corresponding to the arcs (cāpas) c_m and c_n, then the product of the chords is given by
J_m J_n= [J ( (c_m+ c_n)/2)]^2- [J ( (c_m- c_n)/2)]^2 (10)In the above relation since the product (saṃvarga) of two chords (jyās) appear in the LHS, it may be referred to as jyāsaṃvarga-nyāya .
3.1 Recurrence relation from Jyāsaṃvarga-nyāya:
Having described the two theorems with the necessary geometrical construction in great detail , the commentator Śaṅkara Vāriyar proceeds to explain how the jyāsaṃvarga-nyāya can be used to obtain a recurrence relation, which in turn can be used to construct the tabular Rsines—generally referred to as jyānayana or jyotpatti.
The verse that presents the recurrence relation goes as follows [1, 350]:
तत्तज्ज्यावर्गमाद्यज्यावर्गहीनं हरेत् पुनः ।
आसन्नाधस्थशिञ्जिन्या लब्धा स्यादुत्तरोत्तरा ॥ The square of each of the Rsine [starting from the second Rsine] diminished by the square of the first Rsine, may again be divided by the Rsine that is immediately below it. The result obtained would give the successive values of the Rsine one after the other.
To understand the content of this verse, let’s consider a geometrical construction (see Figure 3). In fact Figure 3 is akin to Figure 2. All that has been done to obtain Figure 3 is to complete the circle and mark the center as O. We have also denoted the angle subtended by the chords AC and GB at the center as α and β respectively. It can be easily seen from Figure 3 that
∠AOB =∠AOH+∠HOB=(α+β)/2,
And
∠BOC =∠HOC+∠HOB=(α-β)/2. (11)

Figure 3: Geometrical construction for finding the successive sine values.
Now shifting from arcs and chords to angles and sines, the relation given by (10) expressed as
sin〖α *sin〖β=[sin((α+β)/2) ]^2- [sin((α-β)/2) ]^2. (12) 〗 〗
If we make the substitution,
α=(n+1)θ and β=(n-1)θ (13)
It immediately leads to the relation ,
〖 sin〗(n+1)θ*sin〖(n-1)θ=sin^2〖nθ-sin^2〖θ. (14)〗 〗 〗
To present the above relation in terms of jyās (to be more precise ardhajās) the Rsine values expressed in minutes), as is usually expressed in Indian texts, we replace sine by Rsine by the above equation. Thus we have,
Rsin(n+1)θ*Rsin (n-1)θ=(Rsin nθ)^2-(Rsin nθ)^2.
Rewriting the above, we have
Rsin (n+1)θ=((R sinnθ )^2-(Rsinθ)^2)/(Rsin(n-1)θ) . (15)
This is precisely the relation that relation that is given in the verse quoted above. Using (15), the entire sine table can be constructed by putting in successive values of ‘n’ starting with n = 2 and increasing up to n = 23. For instance, putting n = 2 in (15) we have
Rsin 3θ=((R sin2θ )^2-(Rsinθ)^2)/Rsinθ .
Once we know the value of the first two jyās (Rsin θ and Rsin 2θ) we get the third, and in turn the entire table can be constructed using (15). When we put n = 23, in (15), we get the last jyā which is trijyā (R). This is given by
Rsin 24θ=((R sin23θ )^2-(Rsinθ)^2)/Rsin22θ
The substitution given by (13) obviously imposes constraint on the values of α and β that they can only be integral multiplies of θ. But such a constraint is of little consequence as there is no restriction in the choice of the value of θ. We can choose it as small as we desire, and then proceed with the construction of the sine table . However, this interval is generally chosen to be 3^o 45′ (i.e θ=225′) which is equal to 1/(8 )th of rāśi (30^o).
In fact, the commentary explicitly mentions this [1, 350]:
राश्यष्टम्मंशज्यानयनमपि सुकरमेवIt is indeed easy to obtain the tabular Rsines corresponding to 1/8th of rāśi [using this relation].
No Rsine(x) Angles in degree Śaṅkara’s values of Jyā Āryabhaṭa’s value of Jyā Modern value of Jyā (A) (3438 x sin (A))
- Rsin x 03° 45′ 225′ 225′ 224.8560
- Rsin 2x 07° 30′ 449′ 449′ 448.7490
- Rsin 3x 11° 15′ 671′ 671′ 670.7205
- Rsin 4x 15° 00′ 890′ 890′ 889.8199
- Rsin 5x 18° 45′ 1105′ 1105′ 1105.1089
- Rsin 6x 22° 30′ 1315′ 1315′ 1315.6656
- Rsin 7x 26° 15′ 1520′ 1520′ 1520.5885
- Rsin 8x 30° 00′ 1717′ 1719′ 1719.0000
- Rsin 9x 33° 45′ 1907′ 1910′ 1910.0505
- Rsin 10x 37° 30′ 2088′ 2093′ 2092.9218
- Rsin 11x 41° 15′ 2261′ 2267′ 2266.8309
- Rsin 12x 45° 00′ 2423′ 2431′ 2431.0331
- Rsin 13x 48° 45′ 2574′ 2585′ 2584.8253
- Rsin 14x 52° 30′ 2714′ 2728′ 2727.5488
- Rsin 15x 56° 15′ 2842′ 2859′ 2858.5925
- Rsin 16x 60° 00′ 2957′ 2978′ 2977.3953
- Rsin 17x 63° 45′ 3059′ 3084′ 3083.4485
- Rsin 18x 67° 30′ 3148′ 3177′ 3176.2978
- Rsin 19x 71° 15′ 3222′ 3256′ 3255.5458
- Rsin 20x 75° 00′ 3282′ 3321′ 3320.8530
- Rsin 21x 78° 45′ 3328′ 3372′ 3371.9398
- Rsin 22x 82° 30′ 3359′ 3409′ 3408.5874
- Rsin 23x 86° 15′ 3375′ 3431′ 3430.6390
- Rsin 24x 90° 00′ 3375′ 3438′ 3438.0000
Table 2: Tabular R sine values given by Śaṅkara and Āryabhaṭa
The table 2. contains angles in degrees, the Rsine values calculated from the formula given by Śaṅkara and the Rsine values given by Āryabhaṭa compared with the modern sine values multiplied by R value equal to 3438. This value of radius of the base circle has been taken as a basic parameter for the construction of sine tables in most of the Indian astronomical works.
Here the sine or Jyā of an angle is not a ratio of numbers [8, 405-408]. It constitutes the length of a certain line segment.
The difference in the column 4 and column 5 are minimal. Āryabhaṭa’s iterative formula for generating sine values involves an approximation. In order to have a balance between the accuracy and practicality, Āryabhaṭa would have rounded off certain values for convenience.
Conclusion
In this paper we discussed an interesting method of obtaining tabular Rsines. Here it may be pointed out that Indian astronomers and mathematicians did not merely use tabular Rsines and interpolation techniques to determine the value of sine function but also attempted to obtain approximation to directly compute the sine values for any different arguments. For instance, Bhāskara I in 7th century gives the following rational approximation:
sin〖θ= (4θ(180-θ))/(4050-θ(180-θ)).〗
This is indeed a brilliant approximation that at once captures the symmetry of the function and also yields values that are 90 percent accurate for the entire range 0-180^o. Their continuous efforts to improve upon the accuracy of the obtaining the sine values, has also led them to arrive at the infinite series for sine function [9, 2], discovered by Mādhava in 14th century, almost three centuries before it was reinvented by Newton in 17th century. Arriving at the infinite series, apart from being a landmark achievement in the area of pure mathematics, has also enabled Mādhava to come up with a sine table that is accurate to thirds [4, 64].
Thus it is evident that Indian astronomers and mathematicians have not confined their approaches to construction of sine tables but also have attempted to obtain good rational approximations to directly compute the sine values for different arguments. Currently efforts should be made to highlight such important discoveries made in India as a part of the school curriculum. Scientific and cultural history of India must be introduced and taught in an appealing way to young minds to preserve our heritage and scientific contributions.
Acknowledgements:
I would like to sincerely thank Prof. K. Ramasubramanian, IIT Bombay and Prof. Aditya Kolachana, IIT Madras for discussions, valuable suggestions and comments on this article.
References:
[1] Śaṅkara Vāriyar, Kriyākramakarī, a commentary on Līlāvatī of Bhāskarācārya, ed. . by K. V. Sarma, VVVBIS and Indological Studies No.66, Panjab University, Hoshiarpur, 1975.
[2] Jyeṣṭadeva, Gaṇita-yutkti-bhāṣā, ed. And tr. K. V. Sarma, with detailed explanatory notes by K. Ramasubramanian, M. D. Srinivas and M. S. Sriram, 2 vols, Hindustan Book Agency, New Delhi, 2008, repr. Springer, 2009.
[3] Nīlakaṇṭa Somayājī, Tantrasaṅgraha, with commentaries Yuktidīpikā and Laghuvivṛti of Śaṅkara Vāriyar, ed . by K. V. Sarma, VVBIS and Indological Studies No 10, Panjab University; Hoshiarpur, 1977.
[4] Nīlakaṇṭa Somayājī, Tantrasaṅgraha, with English tr. And explanatory notes by K. Ramasubramanian and M. S. Sriram, Hindustan Book Agency, New Delhi, 2011, repr. Springer, 2011.
[5] Sine of eighteen degrees in India up to the Eighteen century, R. C. Gupta IJHS Vol II No. 1, 1976.
[6] Er. Venugopal Heroor, “Bhāskara Virachita Jyotpatti”, Karnataka Historical Research Society, Dharwad 2005.
[7] Kripa Shankar Shukla and K V Sarma (1976). Aryabhatiya of Aryabhata (Critically edited with Introduction, English Translation, Notes, Comments and Index). Delhi: Indian national Science Academy.
[8] Katz, Victor J., ed. (2007). The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook. Princeton: Princeton University Press ISBN 978-0-691-11485-9.
[9] Bag, A.K. (1976). “Madhava’s sine and cosine series”. Indian Journal of History of Science. 11 (1). Indian National Academy of Science: 54–57.
